Today, I was studying about random numbers generators in javascript then suddenly my mind got strike-out by a question: Since a computer is a deterministic machine, it works on different algorithms that are defined and do not contain any randomness, then how can a machine like a computer generate randomness?

So, I studied a bit about randomness in computers and programs and got to know about something called "Pseudo-random numbers". And, getting to know about this was interesting.

This blog post dives deep into the world of pseudo-random number generators, shedding light on how computers create the illusion of randomness, revealing the common thread of the "seed" that determines everything.

I hope you will learn something new from this blog, If you like it then share it with your friends who are curious to learn about computing :)

Introduction

In the digital age, randomness is a crucial element in various applications, from gaming to cryptography. But have you ever wondered how computers generate random numbers? When we observe the physical world we find random fluctuations everywhere. We can generate truly random numbers by measuring random fluctuations, known as noise. When we measure this noise, known as sampling, we can obtain numbers. - For example, if we measure the electric current of TV static over time, we will generate a truly random sequence.

We can visualize this random sequence by drawing a path that changes direction according to each number, known as a random walk. Notice the lack of pattern at all scales. At each point in the sequence, the next move is always unpredictable. Random processes are said to be nondeterministic since they are impossible to determine in advance. Machines, on the other hand, are deterministic. Their operation is predictable and repeatable.

The Quest for True Randomness

In the digital realm, randomness is an essential ingredient. Whether you're rolling virtual dice in a game or securing sensitive data with encryption, the need for randomness in computing is undeniable. But here's the catch: computers, at their core, are incredibly deterministic machines. They follow instructions and perform calculations, making it impossible to generate true randomness using mathematical algorithms alone.

How to Achieve True Randomness:

Achieving true randomness on a computer is akin to catching lightning in a bottle. Computers must rely on external sources, such as mouse position on the screen, CPU load, battery levels, atmospheric noise, or quantum properties, which are inherently unpredictable. These sources provide the "seed" for generating pseudo-random numbers, creating sequences that appear random but are ultimately rooted in physics.

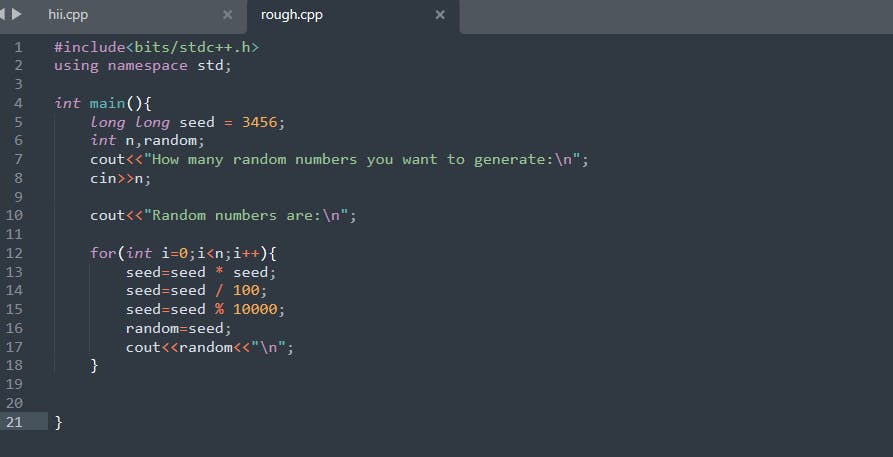
Steps to get pseudo-random numbers:

1. First, select a truly random number, called the "seed".

2. Multiply the seed by itself, and then output the middle of this result.

3. Then you use this output as the next seed.

4. Repeat the process to generate a sequence of pseudo-random numbers.

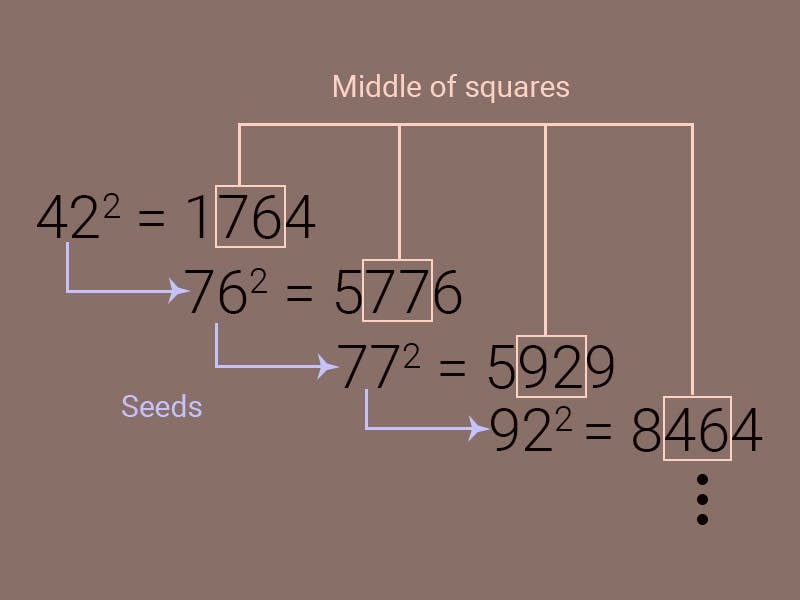
This is known as the middle-squares method and is just the first in a long line of pseudorandom number generators. The randomness of the sequence is dependent on the randomness of the initial seed only. Same seed, same sequence. So, what are the differences between a randomly generated versus pseudorandomly generated sequence? Let's represent each sequence as a random walk.

They seem similar until we speed things up. The pseudorandom sequence must eventually repeat. This occurs when the algorithm reaches a seed it has previously used, and the cycle repeats. The length, before a pseudorandom sequence repeats, is called "the period". The period is strictly limited by the length of the initial seed.

For example, if we use a two-digit seed, then an algorithm can produce, at most, 100 numbers, before reusing a seed and repeating the cycle. A three-digit seed can't expand past 1,000 numbers before repeating its cycle, and a four-digit seed can't expand past 10,000 numbers before repeating. However, if we use a seed large enough, the sequence can expand into trillions and trillions of digits before repeating.

However, the key difference is important. When you generate numbers pseudorandomly, many sequences cannot occur. For example, if Alice generates a truly random sequence of 20 shifts, it's equivalent to a uniform selection from the stack of all possible sequences of shifts. This stack contains 26 to the power of 20 pages, which is astronomical in size.

If we stood at the bottom and shined a light upwards, a person at the top would not see the light for around 200,000,000 years. Compare this to Alice generating a 20-digit pseudorandom sequence, using a four-digit random seed. Now, this is equivalent to a uniform selection from 10,000 possible initial seeds, meaning she can only generate 10,000 different sequences, which is a vanishingly small fraction of all possible sequences.

When we move from random to pseudorandom shifts, we shrink the key space into a much, much smaller seed space. So, for a pseudorandom sequence to be indistinguishable from a randomly generated sequence, it must be impractical for a computer to try all seeds and look for a match. This leads to an important distinction in computer science, between what is possible, versus what is possible in a reasonable amount of time.

We use the same logic when we buy a bike lock. We know that anybody can simply try all possible combinations until they find a match and it opens. But it would take them days to do so. So, for eight hours we assume it's practically safe. With pseudorandom generators, the security increases as the length of the seed increases.

If the most powerful computer would take hundreds of years to run through all seeds, then we safely can assume it's practically secure, instead of perfectly secure. As computers get faster the seed size must increase accordingly. Pseudorandomness frees Alice and Bob from having to share their entire random shift sequence in advance.

Instead, they share a relatively short random seed and expand it into the same random-looking sequence when needed. But what happens if they can never meet to share this random seed?

Thanks for reading and investing your crucial time for my blog, hope you learnt something new and interesting from this blog :)